Faire / Fabriquer

 Corde Ă 13 nĹuds
Corde Ă 13 nĹuds
D 23 octobre 2016
Une corde Ă 13 nĹuds est très facile Ă fabriquer et peut servir Ă beaucoup de calculs et de mesures : mesurer la largeur d'une rivière, la hauteur d'un arbre, faire des triangles, des carrĂŠs, des rectangles, des angles droits... C'est avec une corde Ă 13 nĹuds qu'ont ĂŠtĂŠ dessinĂŠs la forme des clochers par exemple.
Une corde Ă 13 nĹuds se fabrique en faisant 13 nĹuds Ă une corde, tous très prĂŠcisĂŠment espacĂŠs de la mĂŞme distance, quelle qu'elle soit ; ce qui donne 12 intervalles, 12 unitĂŠs de longueur. On coupe les bouts de la corde pour avoir un nĹud Ă chaque extrĂŠmitĂŠ. Il suffit de relier les deux nĹuds de chaque extrĂŠmitĂŠ (dans la mĂŞme main par exemple) pour avoir une corde magique ; celle-ci peut alors former un triangle isocèle de 4-4-4 (attention : ce sont les espaces qui comptent, pas les nĹuds : la corde n'a pas 13 nĹuds, elle a 12 espaces, 12 longueurs), la forme des clochers avec un triangle de 2-5-5, un angle droit avec un triangle de 3-4-5, un rectangle de 2-4-2-4, ou un carrĂŠ de 3-3-3-3. On peut mĂŞme tracer des cercles, en prenant le nĹud correspondant au demi-diamètre dĂŠsirĂŠ.
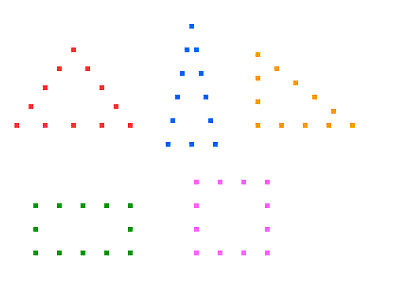

En rouge, un triangle ĂŠquilatĂŠral : 4-4-4.
En bleu, un triangle isocèle, la forme d'un clocher d'Êglise : 2-5-5.
En jaune, un triangle-rectangle, formant un angle droit : 3-4-5.
En vert, un rectangle : 2-4-2-4.
En rose, un carrĂŠ : 3-3-3-3.
On peut aussi en faire de diffĂŠrentes longueurs, par exemple une petite dont les 13 nĹuds tiennent pile dans un seul intervalle d'une plus grande il faudrait alors 12 petites cordes pour en remplacer une grande ; ce qui peut permettre des mesures beaucoup plus prĂŠcises.
Dans mes innombrables notes, je possède le contenu d'une page internet qui explique comment mesurer la largeur d'une rivière Ă l'aide d'une simple corde Ă 13 nĹuds et de jalons plantĂŠs en terre ; mais comme souvent, elle est mal expliquĂŠe et le dessin n'arrange pas les choses. Aussi j'ai essayĂŠ de faire un dessin plus clair et j'espère vous donner ici des explications ĂŠgalement plus claires.
Dans l'absolu, le principe est juste, mais on ne comprenais rien au dessin d'origine parce que toutes les dimensions ĂŠtaient identiques. C'est pourquoi j'ai fait chaque dimension diffĂŠrente pour qu'on s'y retrouve.
J'ai repris le texte d'origine en l'arrangeant au mieux. RĂŠfĂŠrez-vous Ă mes dessins ci-dessous, que j'ai refait aussi (dans cet exemple, on prendra les distances entre chaque nĹud de 1 m pour faire simple).
SchĂŠma 1
Cherchez un point A remarquable sur la rive opposÊe, le plus au bord possible (un arbre, un gros caillou, une fleur, le coin d'une pile de pont, etc.). Plantez bien en face (c'est ça le plus difficile), sur le bord de votre rive, un jalon B, puis un autre bien alignÊ C [le jalon C peut être à n'importe quelle distance du jalon B, mais il doit être dans l'alignement A-B ; ici, par exemple, je l'ai mis tout près. En fait, ce jalon C ne sert que pour calculer l'angle droit sans descendre dans la rivière si le jalon B est juste au bord de l'eau ; mais s'il en est ÊloignÊ, on n'a plus besoin du jalon C puisqu'on peut calculer l'angle droit entre le jalon B et la rivière].


SchĂŠma 1
SchĂŠma 2
Avec votre corde Ă 13 nĹuds, tracez une ligne d'ĂŠquerre [en clair, une ligne Ă angle droit avec le jalon B, en utilisant le triangle jaune 3-4-5 du premier dessin] et implantez des jalons D et E de sorte que BD = DE [BD et DE doivent avoir obligatoirement la mĂŞme longueur ; ici, elles mesurent 10 m (10 longueurs entre 11 nĹuds)].
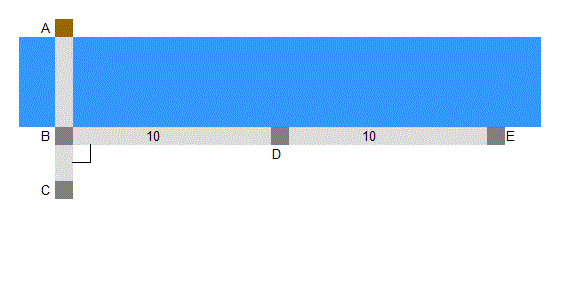

SchĂŠma 2
SchĂŠma 3
Toujours avec la corde Ă 13 nĹuds, tracez une autre ligne d'ĂŠquerre issue de E [tracez une autre ligne Ă angle droit partant du jalon E].
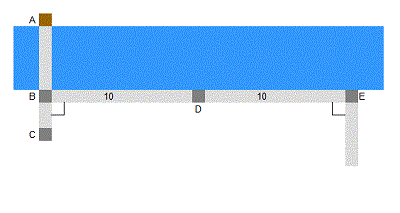

SchĂŠma 3
SchĂŠma 4
Sur cette nouvelle ligne, implantez un jalon F qui s'aligne avec les jalons A et D [ce triangle DEF est le mĂŞme que le premier triangle ABD, mais inversĂŠ ; c'est pourquoi les lignes BD et DE doivent ĂŞtre de dimension identique, ce nouveau triangle inversĂŠ est juste fait pour pouvoir le mesurer en ĂŠvitant de plonger dans la rivière]. La distance EF est la largeur de la rivière, que vous n'avez plus qu'Ă mesurer avec votre corde Ă 13 nĹuds [ou de prĂŠfĂŠrence avec un instrument de mesure plus prĂŠcis ; on voit que, dans cet exemple, elle mesure 6 m].
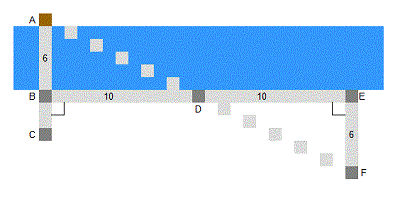

SchĂŠma 4
Quand on implante le jalon B, ce n'est pas obligĂŠ qu'il soit au bord de la rive, il peut en ĂŞtre ĂŠloignĂŠ (dans ce cas, je vous conseille un minimum de 3 longueurs, ou 4 nĹuds, parce que le triangle 3-4-5 fait un minimum de 3 longueurs) ; et une fois qu'on aura trouvĂŠ la distance EF, il faudra penser Ă soustraire la distance entre la rive et le jalon B pour avoir la mesure correcte.
C'est un excellent exemple d'utilisation de la corde Ă 13 nĹuds, mĂŞme s'il n'est pas ĂŠvident, puisque c'est grâce Ă la corde Ă 13 nĹuds qu'on a pu faire un angle droit et tracer ainsi toutes les lignes.
De la même façon, on peut mesurer la hauteur d'un arbre, mais je n'ai plus en tête le processus prÊcis pour vous l'expliquer actuellement...
J 26 octobre 2017
Je pense que, au lieu d'un nĹud, qui fait toujours une bosse et qui est gros et pas facile Ă intĂŠgrer dans des mesures prĂŠcises, on ferait mieux de faire une marque, une simple marque Ă l'encre ou similaire, ainsi cette marque pourrait ĂŞtre beaucoup plus prĂŠcise et permettre des mesures ĂŠgalement plus prĂŠcises, surtout quand on doit mettre un nĹud juste derrière un baton pour faire un angle. Ce serait une sorte de ÂŤ corde Ă 13 marques Âť !
Pas de formulaire de contact pour le moment car j'en cherche un qui contient un captcha et qui fonctionne.
Ne m'écrivez pas : ce formulaire est en cours de test et ne fonctionne pas encore.
()